勉強がてら、やってみました。
SIRモデルのパラメータの推定は、オーソドックスには最尤推定などが用いられるようですが、今回はベイズで定式化して、ベイズ推定もやってみました。
国別のデータを使った分析は最近よく見ますので、今回は以下のデータを使って、都道府県別の感染流行の予測を行ってみます。
https://github.com/kaz-ogiwara/covid19
上記のデータは日々更新されていっているみたいですが、実際にこの記事を書いた時点では、2020年4月23日までのデータを使っています。
Kaggleのノートブック環境を使いました。
コードは以下のノートブックまたはGithubに入っています。
https://www.kaggle.com/itoeiji/covid-19-predictions-bayesian-sir-japan-prefs
SIRモデル
SIRモデルは以下の通り、感染症の流行の振る舞いを記述するモデルで、結構古く（1927）からあるらしいです。
https://ja.wikipedia.org/wiki/SIR%E3%83%A2%E3%83%87%E3%83%AB
インフルエンザや麻疹などの感染症がどのように流行っていくのかといった、疫学的な使い方が主かと思いますが、
一方で、一部ではツイッターなどのSNS上の流行がどのように広まって、やがて落ち着くのかみたいなものにも応用されることがあるみたいです。
（コロナデータ分析してみた流行もなんか当てはまりそう←）
最尤推定でパラメータを推定・予測してみる
データは上記の記載したリポジトリのうちの prefectures.csv 使用しました。
都道府県別に、感染数・回復数・死亡数が時系列で格納されています。
上記データで、I＝感染者数、R＝回復数＋死亡数として、まずは最尤推定でパラメータを推定し、流行予測をプロットしてみました。
以下の記事で各国のデータで行っていましたので、こちらを参考にしました。
【SIRモデル入門】COVID-19データフィッティングで各国終息時期を予測する♬
SIRモデルや尤度関数は、scipyの odeint や minimize を使って、以下のように定義できます。
|
1 2 |
from scipy.integrate import odeint from scipy.optimize import minimize |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def sir(y, t, beta, gamma): dydt1 = -beta * y[0] * y[1] dydt2 = beta * y[0] * y[1] - gamma * y[1] dydt3 = gamma * y[1] return [dydt1, dydt2, dydt3] def estimate(ini_state, beta, gamma): y_hat = odeint(sir, ini_state, ts, args=(beta, gamma)) est = y_hat[0:int(t_max / dt):int(1 / dt)] return est[:, 0], est[:, 1], est[:, 2] def likelihood(params): # params = [beta, gamma] _, I_est, R_est = estimate(ini_state, params[0], params[1]) return np.sum((I_est - I_obs)**2 + (R_est - R_obs)**2) |
パラメータの初期値を設定して最適化すれば以下のようにデータと照らし合わせてパラメータを推定することができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
mnmz = minimize(likelihood, [beta, gamma], method="nelder-mead") # optimize logscale likelihood function mnmz # final_simplex: (array([[2.10745810e-05, 1.34854825e-02], # [2.10745895e-05, 1.34855568e-02], # [2.10745782e-05, 1.34855281e-02]]), array([1044420.1082515 , 1044420.10825449, 1044420.10830346])) # fun: 1044420.1082515011 # message: 'Optimization terminated successfully.' # nfev: 135 # nit: 69 # status: 0 # success: True # x: array([2.10745810e-05, 1.34854825e-02]) |
これでいうと、x[0] が感染率、 x[1] が除去率になりますね。
ベイズ推定でパラメータを推定・予測してみる
次に本命としてやってみたかったこと。
ベイズでSIRモデルを表現して、感染率、除去率、予測の事後分布を推定してみます。
これに関しては以下の論文が同じようなことに挑戦していたので、これを真似してみました。
Contemporary statistical inference for infectious disease models using Stan
Stanでは integrate_ode 関数で微分方程式の計算を表すことができるよう。
これに則って、感染者数、除去者数がポアソン分布に従って発生するとして、以下のようなモデルにしてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
model_code = """ functions { real[] sir( real t, real[] y, real[] theta, real[] x_r, int[] x_i ) { real dydt[3]; dydt[1] <- - theta[1] * y[1] * y[2]; dydt[2] <- theta[1] * y[1] * y[2] - theta[2] * y[2]; dydt[3] <- theta[2] * y[2]; return dydt; } } data { int<lower=1> T; int<lower=1> T_pred; real Y0[3]; int I_obs[T]; int R_obs[T]; real T0; real TS[T+T_pred]; } transformed data { real x_r[0]; int x_i[0]; } parameters { real<lower=0, upper=1> beta; real<lower=0, upper=1> gamma; } transformed parameters { real y_hat[T+T_pred, 3]; real theta[2]; theta[1] = beta; theta[2] = gamma; y_hat <- integrate_ode(sir, Y0, T0, TS, theta, x_r, x_i); } model { real lambda_i[T]; real lambda_r[T]; theta[1] ~ normal(1e-6, 1e-3); theta[2] ~ normal(1e-3 ,1e-3); for (t in 1:T) { lambda_i[t] = y_hat[t ,2]; lambda_r[t] = y_hat[t, 3]; } I_obs ~ poisson(lambda_i); R_obs ~ poisson(lambda_r); } """ |
これをMCMCで解いて、 y_hat, beta, gamma から予測、感染率、除去率のサンプリングを得ます。
いくつかの都道府県について、流行を予測した図が以下の通り。
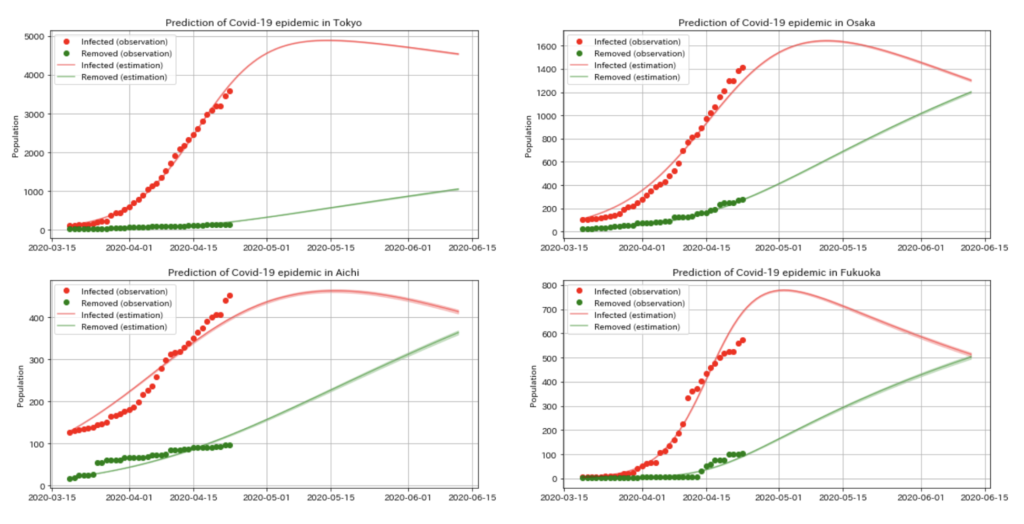
まあまあ、東京や大阪に関しては、データ数も多く、そもそも報告の結果も滑らかになっていたためか、とてもフィットしているように見えます。
これによれば、東京・大阪ともに、ゴールデンウィークの終わり頃にピークに達した後に徐々に収束に向かうような感じになりました。
愛知、福岡に関しては、あまりフィットしていなさそう。
結構、このモデルで表現される振る舞い自体に強い条件がついていそうな気がします。
システム変数的なものも、ちゃんと推定した方が良いのかなと思いました。
回復率の事後分布は以下です。
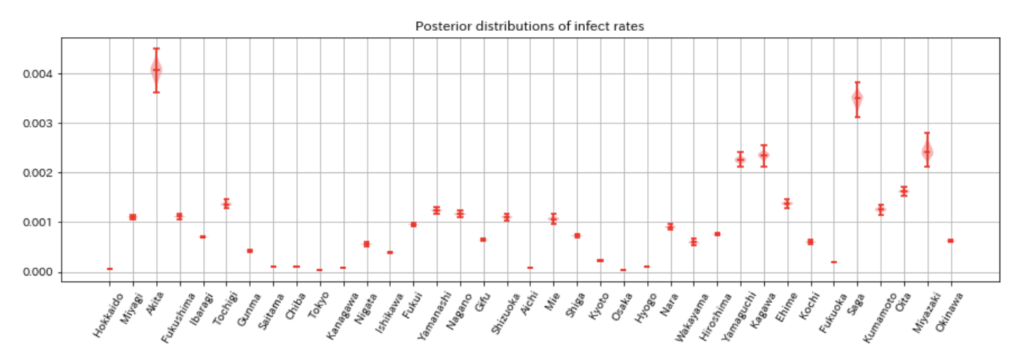
全都道府県でデータが取れているわけではないので、わずかでもデータが取れていた都道府県に限定しています。
ただし、感染率が高いと出ているような都道府県は、事後分布の帯も広く、調べてみるとデータ数を少し少なめ。
また、人数が多い都道府県の感染率が低いという傾向が見られます。
S自体を入力しているわけではないのですが、ちゃんとこの辺りの人数に関係して推定しているのでしょうか。
除去率の事後分布は以下になります。
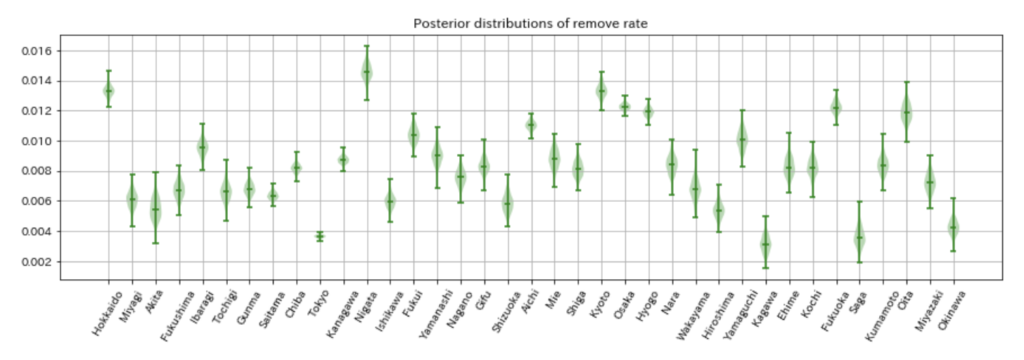
報告を見てても思ってましたが、東京が人数や感染者数に対して、あまり除去されていない感じでした。
“SIRモデルで新型コロナウイルスの感染者数の収束を予測してみた” への 0 件のフィードバック